Question:

I’m trying to implement a Naive Bayes model following the Bayes’ theorem. The problem I face is that some class labels are missing when applying the theorem leading to the overall probability estimate to be zero. How to handle such missing classes when using the Naive Bayes model?

Answer:

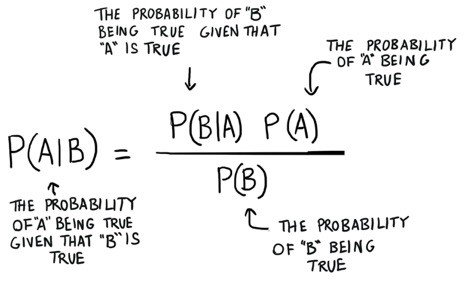
Background. Let first recall what is the Naive Bayes Algorithm. As the name suggests, it is based on the Bayes theorem of Probability and Statistics with a naive assumption that the features are independent of each other.

Bayes Algorithm describes the probability of an event, based on prior knowledge of conditions that might be related to the event.

The assumption of independence of the features is ‘Naive’ because such scenarios are highly unlikely to be encountered in real life.

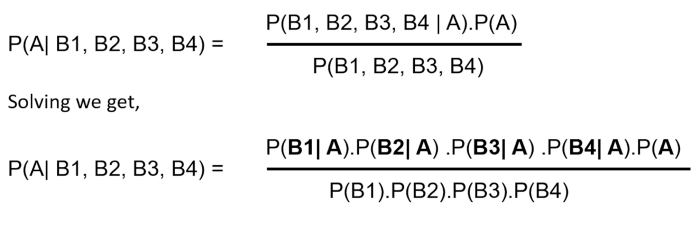
Let us assume that, the event ‘B’ above consists of several sub-events as B1, B2, B3, B4 so the Naive assumption states that the occurrence of B1, B2, B3, B4 is independent of each other, in terms of probability it can be written as:

P(B1, B2, B3, B4) = P(B1).P(B2).P(B3).P(B4)

So, for the above case, the naive assumption can be accommodated in the Bayes theorem:

Example — Let us understand this with an example of email classification as spam or ham (i.e. no spam). We simply count the number of words in both classes of email and then find the probability of each word’s probability given the class prior probability of that email as spam or ham. And then using the Naive Bayes, assuming that the occurrence of each word is independent of each other, we calculate the probability of a new email containing the words ‘friend’, ‘rich’, ‘beach’, ‘money’.

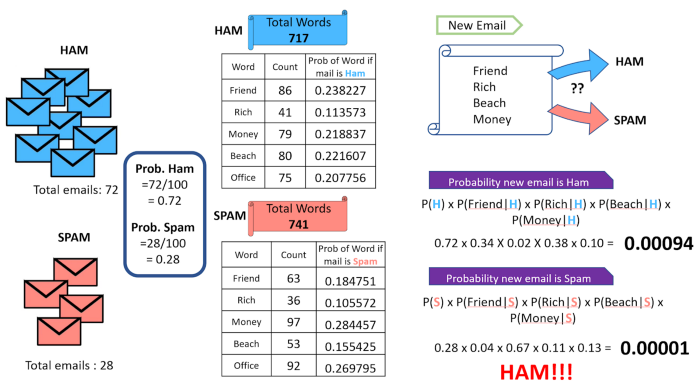
The Zero frequency problem:

If an individual class label is missing, then the frequency-based probability estimate will be zero. And we will get a zero when all the probabilities are multiplied.

In our above example, if the word ‘office’ is missing from the list of words in spam, whenever we see a new email that consists of the word ‘office’ it will always be considered a ham, no matter how ‘spammy’ the other words are.

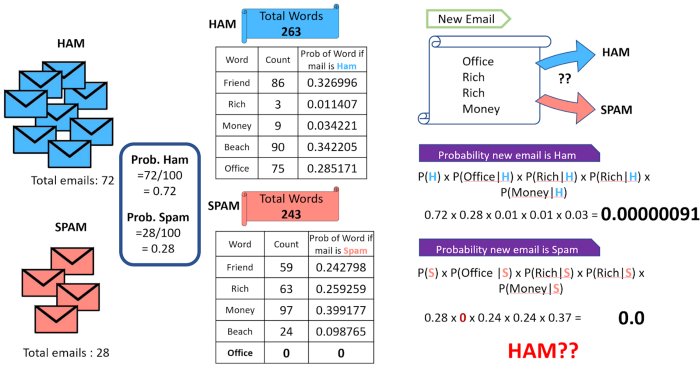
The solution to Zero Frequency Problem:

An approach to overcome this ‘zero-frequency problem’ is to add one to the count for every attribute value-class combination when an attribute value doesn’t occur with every class value.

This will lead to the removal of all the zero values from the classes and, at the same time, will not impact the overall relative frequency of the classes.

In the example above, we increase the value of the word count by 1 for both the spam and the ham emails. Then we calculate the probability of a new email with the words ‘office’, ‘rich’, ‘rich’, ‘money’ as being spam or ham.

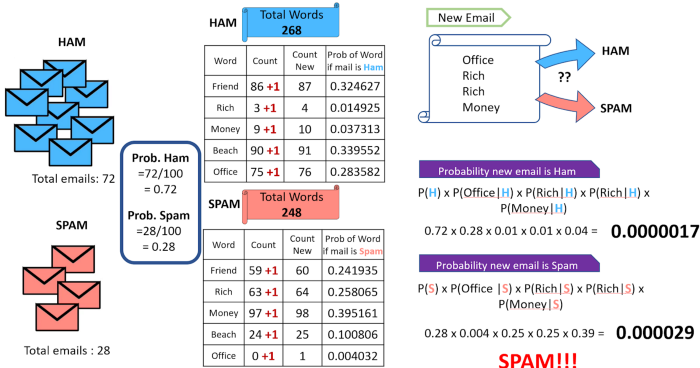
This process of ‘smoothing’ our data by adding a number is known as additive smoothing, also called Laplace smoothing (not to be confused with Laplacian smoothing as used in image processing)

This article is part of the Q&A series by Atoti, where we answer any questions encountered by the data scientist and data analyst community. Is there a question you would like us to answer? Drop us a note!